1.-Introduccin 6n4db
Uno de los problemas clsicos de programacin lineal entera es su utilizacin en la ubicacin de instalaciones. Por lo general estos problemas estn referidos a la minimizacin de los costos de instalacin considerando las restricciones propias del sistema analizado. En el caso presentado en este estudio se expone una variacin al mismo problema, en el cual la funcin objetivo no est definida como minimizacin de la funcin costos, sino como la maximizacin de los atributos que posee cada ubicacin factible de acuerdo a criterios cualitativos de los gerentes. Es decir, cada posible ubicacin posee unas caractersticas de vigilancia, , afluencia, horario e instalaciones que hacen deseables la instalacin de la taquilla en ese sitio, pero que en la situacin problema corresponden a percepciones de los decisores; entonces se quiere plantear una optimizacin en funcin de que las ubicaciones seleccionadas suministren la mayor suma de los valores para estos factores, en funcin de los ndices que representan las preferencias de los tomadores de decisin.
La definicin del nmero de taquillas de paso que sern necesarias para suplir una demanda de los suscriptores se establecer mediante la formulacin, construccin y solucin de un modelo de Programacin Lineal Entera Binaria. Este modelo considerar bsicamente como restricciones: el rea geogrfica de la ciudad en la cual se debe hacer la ubicacin, la competencia de cada agencia comercial, el nmero de suscriptores y la ubicacin de los centros comerciales que pudieran albergar dichas taquillas. El resultado final permiti hacer dicha asignacin y a travs del anlisis de sensibilidad prever la tendencia de funcionabilidad de la solucin al modificarse las condiciones actuales
2.-Objetivos 46304
2.1.-Diagnosticar la situacin actual.
2.2.-Formular un modelo de programacin lineal entera para la solucin del problema.
2.3.-Solucionar el problema.
2.4.-Analizar la solucin obtenida.
2.5.-Analizar la sensibilidad de la solucin.
3.- Bases tericas 1yy4k
3.1.-Programacin lineal 2p2b4a
La Programacin Lineal Entera (PLE) es un tipo de programacin matemtica que se ocupa bsicamente de problemas lineales en los que algunas o todas las variables suponen valores enteros o discretos. El modelo matemtico es sencillamente el mismo modelo de la programacin lineal, con la restriccin adicional de que las variables deben tener valores enteros. Cuando se definen todas las variables como enteras, se dice que el modelo es de Programacin Entera Pura.
Para la solucin de modelos de PLE se utiliza algoritmos recursivos que simplifican, a travs de las cortaduras, la solucin de programacin lineal obtenida. La Tcnica de Ramificacin y Acote es uno de estos algoritmos el cual, se apoya en la idea de divide y vencers. Esto se debe a que, como el nmero finito de soluciones factibles casi siempre es muy grande, resulta demasiado complicado resolver directamente el problema original “grande”. Por esto se divide el problema en sub-problemas cada vez, ms pequeos, hasta que estos se puedan vencer o solucionar. La divisin (ramificacin) se hace mediante una particin del conjunto completo de soluciones factibles en subconjuntos ms pequeos. La conquista (sondeo) se hace en parte acotando la mejor solucin en el subconjunto y despus descartando los subconjuntos cuya cota indique que no es posible que contenga una solucin ptima para el problema original.
3.2.-Metodologa de sistemas blandos de peter checkland 261g1o
La Metodologa de Sistemas Blandos fue creada a finales de los aos 60’s por Peter Checkland, para tratar con los problemas “suaves” (o blandos) de las organizaciones. Un sistema es blando o “suave”, cuando la situacin no est analizada, la identificacin de los recursos es vaga y no se requiere slo buscar informacin sino analizar e identificar las necesidades.
Peter Checkland define esta metodologa como un conjunto de principios o mtodos; los cuales en una situacin particular, guan al tomador de decisiones a elegir un mtodo nico y conveniente a dicha situacin. Esta herramienta al hacer uso del enfoque de sistemas, no pretende sustituir las metodologas existentes para resolver problemas, sino ms bien ser un complemento que permita la generacin y clarificacin del pensamiento.
La estructura de la metodologa comprende siete estadios o etapas e incluye dos tipos de actividades (ver figura 1). Los estadios 1, 2, 5, 6 y 7 son para actividades del “mundo real” donde necesariamente se involucran personas en la situacin problema; y los estadios 3 y 4 son para actividades del “pensamiento de sistemas”, que posiblemente puedan o no involucrar personas en la situacin problema, dependiendo de las circunstancias del estudio.

Para los fines de este trabajo se utilizan los estadios 1 y 2 para estructurar la situacin problema.
Estadio1 y 2: La Expresin y6435
En este estadio se intenta construir la imagen ms rica posible no del “problema”, sino de la situacin en la que se ha percibido un problema. Es la etapa que ms consume tiempo, pues incluye la recoleccin de informacin y presupone el o directo con los grupos que participan en el sistema, para captar los elementos estructurales y de proceso, ms relevantes de la situacin, y la relacin “clima” que exista entre ellos. Es por esto que resulta de importancia su utilizacin ya que nos permite conceptualizar el problema a tratar a partir de una situacin que pareca difusa.
4.-Metodologia 2q662s
En primer lugar la metodologa estuvo orientada hacia la formulacin del problema como tal, lo cual incluye la definicin de las polticas y restricciones del sistema, los recursos disponibles, as como el objetivo de los actores del sistema, a travs de una auditora y la ayuda de la metodologa de Peter Checkland para sistemas blandos.
Con esta informacin se procedi a la segunda etapa de la metodologa la cual estuvo constituida por el modelado a travs de la programacin lineal entera y la utilizacin de la matriz de calificacin de factores para la determinacin de los coeficientes de la funcin objetivo.
4.1-Formulacin y Definicin del Modelo de Programacin Entera 33703k
Corpoelect en Cuman, atiende los requerimientos de sus clientes a travs de sus oficinas Cuman I, Cuman II y Cuman III. El pago por taquilla es el servicio ms demandado en las agencias y es el que origina el mayor trfico de personas en las mismas. La empresa desea disminuir este trfico de personas, a travs de la puesta en marcha de un sistema de taquillas de pago que opere fuera de las agencias comerciales, ubicndolas en centros comerciales y que sea capaz de atender los suscriptores que residen en la ciudad.
Las reas geogrficas, atendidas por las oficinas comerciales, estn conformadas de la siguiente manera:
La agencia Cuman I atiende los pagos de los suscriptores cuyas viviendas o empresas residen en la parte Central y Noroeste de la ciudad, abarcando la zona portuaria ubicada al Norte (conformada por Puertos de Sucre, Conferry y Naviarca, entre otros); la zona comercial del centro, los balnearios tursticos ubicados hacia el Noroeste (entre los que destacan San Luis, Los Uveros y Los Bordones), el Parque Industrial lvaro Bortot (San Luis) ubicado al oeste y las zonas residenciales repartidas a lo largo de cada uno de los sectores descritos.
Por su parte, la agencia Cuman II atiende los pagos de los suscriptores cuyas viviendas o empresas residen tanto en la parte central de la ciudad como en la parte Este de la misma; abarcando as la zona comercial ubicada hacia el Centro Este de la ciudad; el sector residencial emplazado, de Norte a Sur, hacia la parte Este (en el cual se encuentran, entre otros, Caigire, Las Palomas y Cantarrana); la zona pesquera y portuaria del Noreste, el Parque Industrial El Pen ubicado al Este y los terminales terrestre y areo localizados en la parte Centro Norte y Sureste de la ciudad respectivamente.
La agencia Cuman III atiende los pagos de los suscriptores cuyas viviendas y empresas residen en la parte Suroeste de la ciudad; abarcando as las Barriadas ms populosas ubicadas al Suroeste (entre las que destacan La Llanada y Tres Picos); y algunos de los entes gubernamentales como el Ministerio del Ambiente, el Ministerio de Transporte y Comunicaciones, FUNREVI y Obras Pblicas Estadales; localizados hacia el sur de la ciudad.
En la figura 2 se puede observar, las reas atendidas por cada una de las oficinas de recaudacin en la ciudad de Cuman.

Figura 2. Zonas Atendidas por cada Oficina Comercial en Cuman
La ubicacin de las taquillas de paso se restringi a los centros comerciales ms concurridos de la ciudad, los cuales pueden ofrecer comodidades a los clientes en cuanto a la facilidad de , las instalaciones, la vigilancia y el horario de trabajo.
Estos factores fueron los fundamentales para la decisin de ubicacin de las taquillas en los centros comerciales de la ciudad, la dificultad para considerar estos factores es que, como son factores cualitativos y no se posean registros para establecer una medicin precisa que permitiera establecer un ndice para cada uno de ellos y as establecer la funcin objetivo en trminos de estos ndices; adicionalmente cada directivo involucrado en la decisin posea una percepcin diferente sobre las condiciones de: Vigilancia, Instalaciones, Horario, Afluencia y para cada una de las posibles ubicaciones. En funcin de esto se plante un sistema de calificacin para aportar un valor numrico a cada factor, de tal forma que los centros comerciales pudiesen ser evaluados en funcin de cada uno de estos factores.
La calificacin de cada factor se hizo en funcin de una puntuacin del cero (0) al diez (10). Los parmetros de evaluacin se establecieron en funcin de las deficiencias de los centros comerciales, respeto a cada factor. As, una calificacin de diez puntos para una cualidad, representa la carencia de la misma en el centro comercial evaluado. De modo contrario, una calificacin de cero puntos implica que el centro comercial est en condiciones ptimas para instalar una taquilla, de acuerdo a esa cualidad evaluada.
La puntuacin total para cada centro comercial se obtuvo mediante la sumatoria de las calificaciones de cada factor. La puntuacin ms baja ser considerada el mejor resultado (cero puntos), mientras que la evaluacin ms alta ser el peor resultado (cincuenta puntos).
Para la seleccin de los centros comerciales, se consider prudente establecer un rango de aceptacin de calificaciones entre los cero y quince puntos, para asegurar, en promedio, una calificacin individual mnima de cero puntos y una mxima de tres puntos, en cada factor (ver Tabla 1).
Tabla 1: Calificacin de los Factores en cada Centro Comercial
Centro Comercial |
Factores de calidad para los clientes |
|||||
Instalaciones |
Horario |
Vigilancia |
Afluencia |
Puntaje |
||
Express Mall |
2 |
0 |
0 |
0 |
0 |
2 |
Marina’s Plaza |
0 |
0 |
0 |
0 |
2 |
2 |
Gina |
1 |
1 |
1 |
0 |
0 |
3 |
Cristal Plaza |
0 |
1 |
0 |
2 |
1 |
4 |
Don Issa |
2 |
2 |
1 |
1 |
0 |
6 |
San Onofre |
2 |
2 |
1 |
1 |
1 |
7 |
Gran Mariscal |
2 |
1 |
2 |
1 |
1 |
7 |
San Judas |
2 |
2 |
1 |
1 |
1 |
7 |
Patio Andaluz |
3 |
2 |
2 |
2 |
1 |
10 |
El Bosque |
2 |
2 |
1 |
2 |
4 |
11 |
Su Mei |
0 |
0 |
0 |
10 |
4 |
14 |
Karn |
4 |
5 |
1 |
4 |
1 |
15 |
De acuerdo a las ubicaciones de los centros comerciales seleccionados (ver Tabla 2), la Gerencia de Comercializacin ha limitado el nmero de taquillas a instalarse en la ciudad y distribuido por zonas tal limitacin: en las zonas atendidas por la oficinas Cuman I, Cuman II y Cuman III no se deben instalar ms de tres taquillas de paso. Adems, la Coordinacin de la Gestin de las Oficinas Comerciales ha recomendado, para cubrir las expectativas del tipo de cliente, que en el rea comprendida entre las oficinas Cuman I y Cuman II a lo sumo, se instalen seis taquillas.
Para evitar redundancia en cuanto a las ubicaciones de las taquillas, se ha determinado que:
- Si se instala una taquilla en el C.C. Express Mall entonces no debe instalarse taquilla alguna en el C.C. Gina y viceversa. Adems, si se instala una taquilla en el C.C. Gina no debe instalarse taquilla alguna en el C.C. Don Issa y viceversa.
- Si se instala una taquilla en el C.C. Gran Mariscal no debe instalarse taquilla alguna en el C.C. Cristal Plaza y viceversa. Aunado a esto, si se instala una taquilla en el C.C. Cristal Plaza no debe instalarse taquilla alguna en el C.C. Su Mei y viceversa.
Tabla 2: Correspondencia entre las Oficinas y los Centros Comerciales.
Oficina |
Centro Comercial |
Zona |
Cuman I |
Marina’s Plaza |
Noroeste |
Express Mall |
Centro Oeste |
|
Gina |
Centro Oeste |
|
Don Issa |
Centro |
|
Cuman II |
San Onofre |
Centro Este |
Gran Mariscal |
Centro Este |
|
Cristal Plaza |
Noreste |
|
El Bosque |
Este |
|
Su Mei |
Noreste |
|
Cuman III |
San Judas |
Centro Sur |
Karn |
Oeste |
|
Patio Andaluz |
Sur |
A continuacin se muestran, en el mapa de la ciudad de Cuman, los centros comerciales seleccionados:
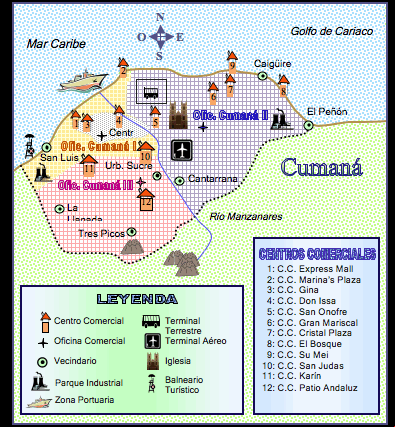
Figura 3: Ubicacin de los Centros Comerciales Seleccionados
Se sabe, mediante histricos manejados por la Coordinacin de la Gestin Comercial de las Oficinas, que el nmero mximo de pagos recibidos en una taquilla en un mes ha sido de 4.986. Estos corresponde a 8 hrs/da * 22 das/mes * 3 min/cliente.
El nmero de suscriptores que demandan las taquillas en relacin a cada oficina comercial se muestra, en la siguiente pgina, en la Tabla.3.
Oficina Comercial |
Nmero de Suscriptores |
Cuman I |
12.405 |
Cuman II |
14.924 |
Cuman III |
13.913 |
La empresa no ha establecido restricciones de costo en cuanto a la instalacin e implementacin de las taquillas. En este sentido, la Direccin Comercial ha establecido que si la empresa presentase dificultades econmicas a la hora de ejecutar el proyecto, esta desarrollara el mismo por etapas para poder cubrir los gastos de forma fraccionada.
La Gerencia de Comercializacin de la Zona Sucre desea determinar en cules de los centros comerciales seleccionados sern las ubicaciones ptimas y garantizar la mayor satisfaccin de los clientes que acudan a ellas, segn los factores sealados como importantes en cada opcin.
4.2.-Construccin del Modelo 3m133m
El modelo formulado gira en torno al nmero de taquillas de paso a instalarse y a la distribucin que deben tener las mismas. Por tal razn, se consider prudente definir las variables de decisin en funcin de instalar o no taquillas de paso, en los centros comerciales seleccionados, para saber luego como quedara la distribucin de las mismas. Como cada decisin deba representarse matemticamente, se acord el uso de variables de decisin binarias que acogieran el valor de uno (1) para la alternativa de instalar una taquilla, en un centro comercial especfico, y cero (0) para la alternativa de no instalar. Con dichas consideraciones se establecieron las siguientes variables de decisin:
Variables de Decisin m6a
X1: Instalar o no una Taquilla de Paso en el C.C. Express Mall.
X2: Instalar o no una Taquilla de Paso en el C.C. Marina’s Plaza.
X3: Instalar o no una Taquilla de Paso en el C.C. Gina.
X4: Instalar o no una Taquilla de Paso en el C.C. Don Issa.
X5: Instalar o no una Taquilla de Paso en el C.C. San Onofre.
X6: Instalar o no una Taquilla de Paso en el C.C. Gran Mariscal.
X7: Instalar o no una Taquilla de Paso en el C.C. Cristal Plaza.
X8: Instalar o no una Taquilla de Paso en el C.C. El Bosque.
X9: Instalar o no una Taquilla de Paso en el C.C. Su Mei.
X10: Instalar o no una Taquilla de Paso en el C.C. San Judas.
X11: Instalar o no una Taquilla de Paso en el C.C. Karn.
X12: Instalar o no una Taquilla de Paso en el C.C. Patio Andaluz.
Donde:

Con i = 1, 2, 3,...., 12
Funcin objetivo 4g583p
Debido a que las variables de decisin consisten en la instalacin o no de una taquilla de paso en un centro comercial especfico, sus coeficientes sern la puntuacin alcanzada por cada centro comercial. La funcin objetivo consistir entonces, en una ecuacin abocada a sumar las deficiencias particulares de cada centro comercial. Por su parte, el modelo tendr como meta minimizar el valor de dicha funcin para asegurar que los resultados comprendan una combinacin ptima de centros comerciales que reduzca las deficiencias de los factores de calidad, de modo que se garantice la satisfaccin de los clientes y, por ende, el xito de las taquillas.
De acuerdo a la tabla 1, se estructur la ecuacin de la funcin objetivo de la siguiente manera:
MINIMIZAR: Z = 2X1 + 2X2 + 3X3 + 6X4 + 7X5 + 7X6 + 4X7 + 11X8 + 14X9 + 7X10 + 15X11 + 10X12
Restricciones 1g2p49
Las restricciones del modelo de Programacin Entera Binaria se han establecido considerndose las zonas atendidas por cada oficina, el nmero de clientes de las mismas, la capacidad del personal de taquilla y la ubicacin de los centros comerciales seleccionados.
- De acuerdo al nmero de taquillas por oficina comercial:
X1 + X2 + X3 + X4 ≤ 3
X5 + X6 + X7 + X8 + X9 ≤ 3
X10 + X11 + X12 ≤ 3
X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 ≤ 6
- De acuerdo al nmero de pagos atendidos por taquilla:
4.986 (X1 + X2 + X3 + X4) ≥ 12.405
4.986 (X5 + X6 + X7 + X8 + X9) ≥ 14.924
4.986 (X10 + X11 + X12) ≥ 13.913
- De acuerdo a la ubicacin de los centros comerciales:
X1 + X3 = 1
X3 + X4 = 1
X6 + X7 = 1
X7 + X9 = 1
- Restricciones de Costo: “No existen”.
- Restricciones de No Negatividad:
0 ≤ Xi ≤ 1 y enteras; Con i = 1, 2, 3,...., 12
5.-Solucin del modelo 6a2a1e
Para la solucin del modelo se empleo el LINDO 6.01.A continuacin se muestra la solucin mostrada en la pantalla inicial del LINDO:

Figura 4: Solucin por Pantalla del LINDO
NEW INTEGER SOLUTION OF 64.0000000 AT BRANCH 0 PIVOT 14
RE-INSTALLING BEST SOLUTION...
OBJECTIVE FUNCTION VALUE
1) 64.00000
VARIABLE VALUE REDUCED COST
X1 1.000000 2.000000
X2 1.000000 2.000000
X3 0.000000 3.000000
X4 1.000000 6.000000
X5 1.000000 7.000000
X6 0.000000 7.000000
X7 1.000000 4.000000
X8 1.000000 11.000000
X9 0.000000 14.000000
X10 1.000000 7.000000
X11 1.000000 15.000000
X12 1.000000 10.000000
6.-Anlisis de la solucin obtenida 662p1k
Los valores obtenidos para las Variables de Decisin se traducen en nueve valores no nulos, o sea, nueve taquillas a instalarse (en los centros comerciales correspondientes a cada una de estas variables); y tres valores nulos para variables en cuyos centros comerciales no se debe instalar una taquilla de paso.
En resumen, se puede decir que, la relacin entre los valores obtenidos para cada variable y las decisiones asociadas (respecto a la instalacin o no de taquillas de paso en los centros comerciales seleccionados, estn condensadas de la forma siguiente:
Tabla 4: Valores de las Variables y las Decisiones t384t
Variable |
C.C. |
Valor |
Decisin |
X1 |
C.C. Express Mall. |
1 |
Instalar |
X2 |
C.C.Marina’s Plaza. |
1 |
Instalar |
X3 |
C.C. Gina |
0 |
No Instalar |
X4 |
C.C. Don Issa. |
1 |
Instalar |
X5 |
C.C. San Onofre. |
1 |
Instalar |
X6 |
C.C. Gran Mariscal. |
0 |
No Instalar |
X7 |
C.C. Cristal Plaza. |
1 |
Instalar |
X8 |
C.C. El Bosque. |
1 |
Instalar |
X9 |
C.C. Su Mei. |
0 |
No Instalar |
X10 |
C.C. San Judas. |
1 |
Instalar |
X11 |
C.C. Karn. |
1 |
Instalar |
X12 |
C.C. Patio Andaluz |
1 |
Instalar |
7.-Anlisis de sensibilidad 184f3l
Debido a que la solucin del modelo fue obtenida en funcin de valores lmites ideales, es necesario corroborar tanto la factibilidad como la optimalidad de la funcin para ciertas variaciones tanto en los valores de cada restriccin (bj), los cuales representan el nmero mnimo de clientes atendidos, como los nmeros de pagos a atenderse por cada taquilla, representados por los coeficientes aij de las variables en la restriccin tres del modelo de PEB planteado.
Variaciones de los bj 2f4rm
Los valores manejados para los bj (ubicados del lado derecho de cada desigualdad), utilizados en la restriccin dos, representan las cantidades mnimas de clientes para el funcionamiento de las taquillas. Para corroborar la factibilidad y optimalidad de la funcin para valores diferentes, se estableci un rango de incremento para el nmero de clientes que oscilar entre el valor de los bj utilizados y un valor mximo equivalente al nmero total de suscriptores de la empresa en la ciudad. En este intervalo, se han seleccionado valores, para la prueba, que representan porcentajes de incrementos de los bj del 25% y 50%. Estos incrementos porcentuales son los manejados por la Coordinacin de la Gestin de las Oficinas Comerciales para evaluar el rendimiento de la afluencia de clientes, a las taquillas de las agencias de recaudacin. A continuacin se muestra el comportamiento de la funcin objetivo con las variaciones antes mencionadas.
Tabla 5: Variacin Porcentual de los bj
Oficina |
N Clientes |
N Taquillas |
Tipo Solucin |
Cuman I |
15.506 (+25%) |
9 |
FACTIBLE/OPTIMA |
18.608 (+50%) |
10 |
NO FACTIBLE |
|
43.162 |
10 |
NO FACTIBLE |
|
Cuman II |
18.655 (+25%) |
9 |
NO FACTIBLE |
22.386 (+50%) |
11 |
NO FACTIBLE |
|
43.162 |
11 |
NO FACTIBLE |
|
Cuman III |
17.391 (+25%) |
9 |
FACTIBLE/OPTIMA |
20.869 (+50%) |
11 |
NO FACTIBLE |
|
43.162 |
11 |
NO FACTIBLE |
Detallando los resultados obtenidos (de acuerdo las restricciones impuestas), por oficina, se tiene que:
- En la Oficina Cuman I, las taquillas de paso son insuficientes a partir de un valor superior al 25 % adicional al bj correspondiente (15.506).
- En la Oficina Cuman II, las taquillas de paso son insuficientes en un valor inferior al 25 % adicional del bj correspondiente (18.655).
- En la Oficina Cuman III, las taquillas de paso son insuficientes a partir de un valor superior al 25 % adicional del bj correspondiente (17.391).
Por esta razn, utilizndose el tanteo, se ha determinado el valor exacto hasta el cual la solucin se hace Factible en los respectivos incrementos de los bj.
Tabla 6: Variacin por Tanteo de los bj
Oficina |
N Clientes |
N Taquillas |
Tipo Solucin |
Cuman I |
15.506 (+25%) |
9 |
FACTIBLE/OPTIMA |
15.517 (+25,08%) |
9 |
FACTIBLE/OPTIMA |
|
Cuman II |
18.655 (+25%) |
9 |
FACTIBLE/OPTIMA |
17.326 (+16,095%) |
9 |
FACTIBLE/OPTIMA |
|
Cuman III |
17.391 (+25%) |
9 |
FACTIBLE/OPTIMA |
17.402 (+25,077%) |
9 |
FACTIBLE/OPTIMA |
Variaciones de los aij 1x624x
El valor manejado para los aij (coeficientes de las variables), de la restriccin dos, representa las cantidades mxima de pagos que se han podido procesar en una taquilla, durante un mes.
Dado que no todas las jornadas de cobro manejan este mximo volumen de transacciones, se consider prudente corroborar la factibilidad y optimalidad de la funcin para valores menores. Para ello, se estableci un rango de decremento para el nmero de pagos recibidos por taquilla de modo de detallar el valor lmite para este valor. El decremento para este valor fue del 10 %, as, se conform la siguiente tabla:
Tabla 7: Variacin Porcentual de los aij
Oficina |
N Pagos |
N Taquillas |
Tipo Solucin |
Cuman I |
4.487 (-10%) |
11 |
FACTIBLE |
3.989 (-20%) |
11 |
FACTIBLE |
|
3.490 (-30%) |
12 |
NOFACTIBLE |
|
2.992 (-40%) |
12 |
NO FACTIBLE |
|
2.493 (-50%) |
134 |
NO FACTIBLE |
|
Cuman II |
4.487 (-10%) |
10 |
NO FACTIBLE |
3.989 (-20%) |
10 |
NO FACTIBLE |
|
3.490 (-30%) |
11 |
NO FACTIBLE |
|
2.992 (-40%) |
12 |
NO FACTIBLE |
|
2.493 (-50%) |
15 |
NO FACTIBLE |
|
Cuman III |
4.487 (-10%) |
12 |
FACTIBLE |
3.989 (-20%) |
12 |
NO FACTIBLE |
|
3.490 (-30%) |
15 |
NO FACTIBLE |
|
2.992 (-40%) |
15 |
NO FACTIBLE |
|
2.493 (-50%) |
15 |
NO FACTIBLE |
Detallando los resultados obtenidos (de acuerdo las restricciones impuestas), por cada oficina comercial, se pueden puntualizar las siguientes afirmaciones:
- En la Oficina Cuman I, las taquillas de paso son insuficientes a partir de un rendimiento menor al 80 % del aij correspondiente (3.989).
- En la Oficina Cuman II, las taquillas de paso son insuficientes a partir de un rendimiento menor al 90 % del aij correspondiente (4.487).
- En la Oficina Cuman III, las taquillas de paso son insuficientes a partir un rendimiento menor al 90 % del aij correspondiente (4.487).
Por esta razn, utilizndose el tanteo, se ha determinado el valor exacto del aij a partir del cual, la solucin se hace Factible.
Tabla 8: Variacin por Tanteo de los aij
Oficina |
N Pagos |
N Taquillas |
Tipo Solucin |
Cuman I |
3.989 (80%) |
11 |
FACTIBLE |
3.986 (79,924%) |
11 |
FACTIBLE |
|
Cuman II |
4.487 (90%) |
10 |
NO FACTIBLE |
4.707 (94,4%) |
10 |
FACTIBLE |
|
Cuman III |
4.487 (90%) |
12 |
FACTIBLE |
4.502 (90,29%) |
11 |
FACTIBLE |
Esto implica que esta propuesta debe mantenerse bajo seguimiento, dado lo ajustado de los resultados a los valores suministrados.
8.- Conclusiones 6b6tx
En conclusin:
8.1.-La Oficina Cuman I contar con tres taquillas de paso las cuales estarn ubicadas en los centros comerciales: Express Mall (en el Centro Oeste de la ciudad), Marina’s Plaza (en el Centro Norte) y en el Don Issa (en el Centro). La Oficina Cuman II, por su parte, contar con tres taquillas las cuales estarn ubicadas en los centros comerciales: San Onofre (en el Centro de la ciudad), El Bosque (al Este) y en el Cristal Plaza (en el Centro Este). Entre tanto, la Oficina Cuman III contar con tres taquilla de paso ubicadas en los centros comerciales: Karn (en el Oeste), Patio Andaluz (al Sur) y en el San Judas en el Centro Sur de la ciudad (ver Anexos C.2, C.3, C.4, C.5, C.6, C.7 y C.8).

Figura 5: Distribucin Final de las Taquillas de Paso.
8.2.- El diagnostico de la situacin permiti obtener la informacin necesaria para la formulacin del modelo, para ello la metodologa de Meter Checkland permiti la comprensin del sistema y la determinacin de los datos necesarios para la formulacin del modelo de Programacin Lineal Entera Binaria.
8.3.- El modelo pudo recoger en su funcin objetivo las variables que los decidores deseaban optimizar, las cuales representaban preferencias subjetivas y para las cuales no se posean ndices de medicin. En este sentido, la calificacin de factores resulto una herramienta de fcil uso y de aceptacin por los s por la visualizacin de sus intereses.
8.4.-La solucin result factible y de conformidad con los factores considerados en la funcin objetivo, para lo cual fueron seleccionadas 9 ubicaciones que cumplieron con las restricciones impuestas al modelo.
8.5.- A travs del anlisis de sensibilidad se pudo determinar la validez de la solucin en funcin de los incremento del volumen de clientes por agencia. Observndose que la agencia mas sensible es Cuman II, quien solo soporta un incremento de s del 16,01
9.-Recomendaciones 2c4p5p
9.1.- La propuesta de instalar taquillas de paso en la ciudad de Cuman es propicia para ser extrapolada a otras ciudades que presenten problemas similares a los hallados en las oficinas estudiadas. Por ello es recomendable que antes de expandir esta propuesta a otras latitudes, las Gerencias de Comercializacin interesadas estudien de forma detallada (al igual que se hizo en la ciudad de Cuman), el funcionamiento del sistema de pago por taquilla para determinar si realmente es meritoria la puesta en marcha de este tipo de pago
9.2.- Una vez puestas en marcha las taquillas, al tiempo que estas hallan generado los datos suficientes en cuanto a los pagos atendidos, se sugiere establecer un anlisis del funcionamiento de las mismas a travs de la Teora de Colas para mantener la calidad del servicio.
10.-Bibliografia 47262q
CADAFE. (2002). “Dossier de la Empresa”, www.cadafe.com.ve/pages/s2.htm,
CADAFE, (1999). “Induccin al rea Comercial”, Direccin Ejecutiva de Coordinacin de Filiales, Caracas,
Chase R. y Aquilano N., (1994). “Direccin y istracin de la Produccin y de las Operaciones”. Sexta Edicin, Editorial Adis - Wesley Iberoamericana, Buenos Aires, Argentina,
Draper J. y Klingman J., (1972). “Matemticas para istracin y Economa”. Primera Edicin, Editorial Tec-Cien, Mxico,
Eppen G., Gould F. y Schmidt C., (1992). “Investigacin de Operaciones en la Ciencia istrativa”. Tercera Edicin, Prentice-Hall Hispanoamericana, Mxico,
Freund J. y Walpole R., (2.000). “Estadstica Matemtica con Aplicaciones”. Cuarta Edicin, Editorial Prentice-Hall Hispanoamericana, Mxico.
Hernndez C., “Adaptacin de un Modelo de Confiabilidad al Sistema Automatizado de Recaudacin de las Oficinas Comerciales que operan en una Empresa de Energa Elctrica en el estado Monagas-Maturn”, Trabajo de Grado presentado para optar al ttulo de Ingeniero de Sistemas, Universidad de Oriente, Barcelona, Venezuela.
Hiller F. y Lieberman G., (1991). “Introduccin a la Investigacin de Operaciones”. Quinta Edicin, Editorial McGraw-Hill, Mxico.
Mrquez W., (2.002). “Estudio Sistmico al Proceso de Facturacin de Compra y Distribucin de Energa, en la Superintendencia de Comercializacin de la Gerencia de Transmisin y Distribucin Elctrica (T&D) de PDVSA Oriente”, Trabajo de Grado presentado para optar al ttulo de Ingeniero de Sistemas, Universidad de Oriente, Barcelona, Venezuela.
Moskowitz H. y Wright G. , (1.982). “Investigacin de Operaciones”. Primera Edicin, Editorial Prentice-Hall Hispanoamericana, Mxico.
Salgado N., (1.997). “Aplicacin de la Reingeniera de Procesos al Sistema de Recaudacin de las Oficinas Comerciales de una Empresa de Energa Elctrica”, Trabajo de Grado presentado para optar al ttulo de Ingeniero de Sistemas, Universidad de Oriente, Barcelona, Venezuela.
Taha H., (1995). “Investigacin de Operaciones”. Quinta Edicin, Editorial AlfaOmega, Mxico.
Universidad Nacional Abierta, (1.990). “Introduccin a la Ingeniera de Sistemas”, Cuarta Edicin, Caracas.
Winston W., (1993). “Investigacin de Operaciones”. Segunda Edicin, Grupo Editorial Iberoamrica, Mxico.